Ukhti of MatH

Senin, 16 November 2009

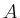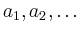A set consists of distinct elements $a_1,a_2,\ldots$ :

$\displaystyle A = \{a_1,a_2,\ldots\}\, .$

If such elements are characterized via a property 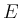, this is symbolized as follows:

$\displaystyle A = \{a:\ a\$ satisfies property $\displaystyle \ E\}\, .$

The following notations are commonly used:

notation	meaning
$a\in A$	is element of
$a\notin A$	is not element of
$A\subseteq B$	is a subset of
$A\subset B$	is a strict subset of
$\vert A\vert$	number of elements in
$\emptyset$	empty set

If 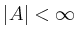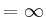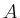$\vert A\vert<\infty$ ( $=\infty$ ), is called a finite (infinite) set.

Two sets are called equipotent, if there exists a bijective map between their elements (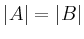 $\vert A\vert=\vert B\vert$ for finite sets 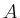and ).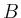

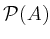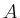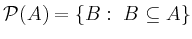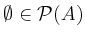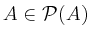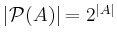The set ${\cal P}(A)$ of all subsets of is called power set, i.e. ${\cal P}(A)=\{B:\ B\subseteq A\}$ . In particular, we have $\emptyset\in {\cal P}(A)$ and $A\in {\cal P}(A)$ . Moreover, $\vert{\cal P}(A)\vert=2^{\vert A\vert}$ .

http://www.mathematics-online.org/kurse/kurs7/seite7.html